Protons, neutrons, and electrons have mass.

m_p = 1.673*10^-27 kg,  m_n =1.675*10^-27  kg,  m_e = 9.109*10^-31 kg.

Massive particles produce gravitational fields and are acted on by gravitational fields.  (Massive particles attract each other.)

A field is a way of explaining action at a distance.  The magnitude of the gravitational field produced by a massive object at a point P is the force per unit mass it exerts on another massive object located at that point.  The direction of the gravitational field is the direction of that force.

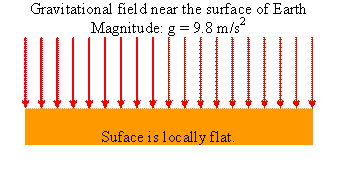
The magnitude of the gravitational force near the surface of Earth is F = mg, the gravitational field has magnitude F/m = g.  Its direction is downward.

Protons and electrons have charge.

q_p = 1.602*10^-19 C, q_e = -1.602*10^-19 C.

Charged particle produce electric fields and are acted on by electric fields.  (Charged particles attract or repel each other.)

The magnitude of the electric field E produced by a charged particle at a point P is the force per unit positive charge it exerts on another charged particle located at that point.  The direction of the electric field is the direction of that force on a positive charge.  The actual force on a particle with charge q is given by F = qE.

Electric field of a positive charge.        A positive test charge is repelled.	Electric field of a negative charge.         A positive test charge is attracted.

The magnitude of the electric field E at a point P is inversely proportional to the square of the radial distance of the point P away from the charge.

Moving charged particles also produce magnetic fields and are acted on by magnetic fields.  Currents are moving charges and produce magnetic fields.   Permanent magnets are the result of magnetization currents flowing inside the material.  For a current flowing in a long straight wire, the magnitude of the magnetic field B at a point P is inversely proportional to the radial distance of the point P away from the wire.  B encircles the wire.  The direction of B is given by the right-hand rule.

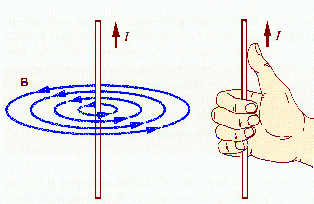
The picture below shows an iron-filing pattern, which reveals the nature of the magnetic field surrounding a current-carrying wire.

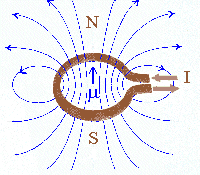
The magnetic field B produced by a current flowing in a coil is shown below.

The magnetic field outside the coil resembles that of a permanent bar magnet shown below and the coil is called an electromagnet.

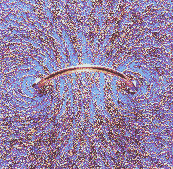
A small current loop also produces a magnetic field.  The field-line pattern is that of a small button magnet.  We say that the loop has a magnetic moment μ = IAn.  Here I is the current flowing in the loop, A is the area of the loop, and n is a unit vector perpendicular to the area.  The direction n of the magnetic moment is again defined by the right-hand rule.  Curl the fingers of your right hand in the direction that the current flows.  Your thumb points in the direction of n.  The magnetic field lines of a loop with dipole moment μ are shown below.  The field-line pattern is that of a small magnet.  We say that μ points from the south pole to the north pole of the magnet.  (Magnetic field lines therefore exit a magnet at the north pole and enter at the south pole.)

The picture below shows the field pattern in a plane perpendicular to the loop, revealed with iron filings.

The magnetic field is a vector.  Magnetic fields produced by different currents sources can enhance each other or cancel out.

Magnetic fields exert forces on other moving charge.  The force a magnetic field exerts on a charge q moving with velocity v is called the Lorentz force.  It is given by

F = qv×B.

The force F is perpendicular to the direction of the magnetic field B.  It also is perpendicular to the direction of the velocity v.  F is perpendicular to the plane that contains both v and B.  The magnitude of F is F = qvBsinθ, where θ is the smallest angle between the directions of the vectors v and B.  If v and B are parallel or anti-parallel to each other, then v×B = 0 and F = 0, since sinθ = 0.  If v and B are perpendicular to each other, then sinθ = 1 and F has its maximum possible magnitude F = qvB.

In an external magnetic field a magnetic moment (a current loop or a magnet) can experience a force and a torque.

The torque τ = μ × B tries to align the magnetic moment with the magnetic field.  Its magnitude is  τ = μBsinθ, where θ is the smallest angle between the directions of the vectors μ and B.  The torque is zero when μ and B are parallel or anti-parallel to each other.

The force tries to pull an aligned dipole into regions where the magnitude of the magnetic field is larger and push an anti-aligned dipole into regions where magnitude the magnetic field is smaller.

If the magnetic field is pointing into the z-direction, the force on a magnetic dipole in that field is given by

F_z = μ_zdB_z/dz.

Here μ_z = μ cosθ is the z-component of the magnetic moment.

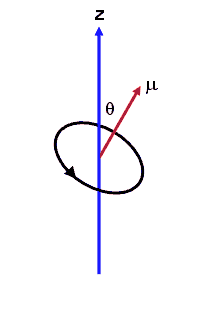
If B is constant, then dB_z/dz = 0 and there is no force.  In an inhomogeneous field where dB_z/dz is not zero, the magnetic dipole experiences a force in the z-direction, unless θ = 90^o and μ_z= 0.  Since for a classical current loop μ can point into any direction the force F_z can have any value from -μdB_z/dz to +μdB_z/dz.

If we passed a beam of magnetic dipoles, which were randomly oriented and could not change their orientation during the passage, through an inhomogeneous magnetic field, different dipoles would be deflected by different amounts.

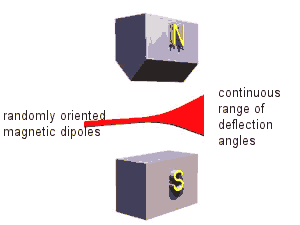
Permanent magnets

Magnetic fields are produced by currents.  Permanent magnets are the result of magnetization currents flowing inside the material.  We may expect that electrons in atoms can have a magnetic moment similar to the magnetic moment of tiny current loops, since they have angular momentum, and angular momentum is usually associated with orbits.  It has been experimentally verified that if electrons in atoms have angular momentum L, then they have a magnetic moment μ that is proportional to L, μ =  γL, with γ = -|q_e|/(2m_e) a constant of proportionality.  Since the orbital angular momentum is quantized, so is the magnetic moment due to orbital angular momentum.  The orbital angular momentum of many electrons with orbital angular momentum L₁, L₂, L₃, ...  adds up to yield the total angular momentum L = L₁ + L₂ + L₃ + ... , and the total magnetic moment μ due to the total orbital angular momentum is proportional to L.

In 1915 Einstein and the Dutch physicist de Haas carried out an experiment to show the link between the angular momentum of atoms and their magnetic moments.  Einstein and de Haas suspended an iron cylinder from a thin fiber inside a coil, where one measures an approximately uniform magnetic field when a current is flowing.  Initially no current is flowing, and the magnetic moments of the individual atoms of the cylinder are randomly oriented, and the cylinder has no net magnetic moment.  However, when a current is switched on, the magnetic field B will exert a torque on the magnetic moments μ of the individual atoms, and they will line up parallel to the magnetic field.  If the angular momentum L of each atom is proportional to μ, then this alignment of the atomic magnetic moments must cause an alignment of the atomic angular momenta, anti-parallel to the magnetic field B because the proportional constant γ is negative.
But angular momentum about an axis is conserved if no external torque about that axis is present.  The total angular momentum L_tot about the direction of the magnetic field remains zero because no external torque about that direction acts on the cylinder.  When B is turned on, the atomic angular momenta line up anti-parallel to B.  So for the total angular momentum to the remain zero, the cylinder starts to rotate around its central axis with the angular momentum of the cylinder parallel to B.

Einstein was a great theoretician, but this was the only experiment he ever published.

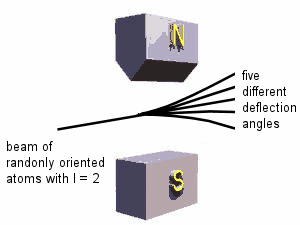
The possible values that we can measure for the square of the magnitude of the orbital angular momentum are L² = l(l+1)ħ².  The possible projections we can measure along any axis, for example the z-axis, are L_z = mħ.  Here l is an integer, l = 0, 1, 2, ... ,  and for a given l, m can take on values from -l to l in integer steps.  Since L_z is quantized, μ_z is quantized, μ_z = -|q_e|mħ/(2m_e) = -μ_Bm.  Here μ_B = |q_e|ħ/(2m_e) is called the Bohr magneton.  If we passed a beam of randomly oriented atoms with orbital angular momentum L through an inhomogeneous magnetic field, we would expect different atoms to be deflected by different amounts depending on the value of μ_z.

F_z = μ_zdB_z/dz.

Since L_z can take on 2l + 1 different values,  μ_z can take on 2l + 1 different values, and we expect 2l + 1 different deflection angles.  Note that 2l + 1 is always an odd integer.

The Stern-Gerlach experiment

In 1921, Otto Stern and Walter Gerlach performed such an experiment.  The actual experiment was carried out with a beam of neutral silver atoms from a hot oven because silver atoms could be readily detected using a photographic emulsion.

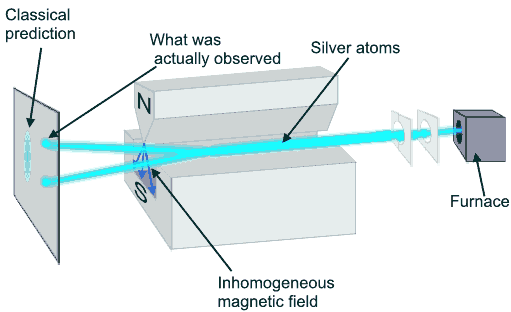
A beam of silver atoms emerges from a furnace held at 1000 K.  It is collimated using 0.1 mm slits, passed between the poles of a magnet, and directed onto a screen, where the atoms are detected.  The speed of the silver atoms is approximately 500 m/s (from (3/2)kT = (1/2)mv², k = 1.38*10^-23 J/K).  In the experiment the silver atoms hit the screen in two distinct spots.  The measurement yields only two possible values for μ_z.

What is going on?

If the magnetic moment of a silver atom was due to the orbital angular momentum of the electrons, an odd number of spots would have to be measured.  However, as we will see in the next module, electrons in silver atoms in their ground state have no net orbital angular momentum.  The magnetic moment of a silver atoms is not due to the orbital angular momentum of its electrons, but due to the spin of one electron.